about

Project abstract

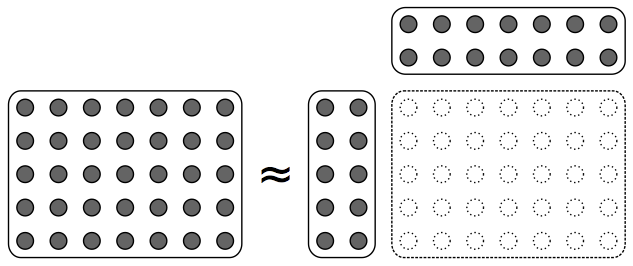
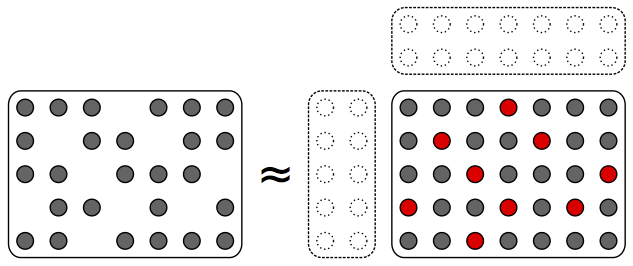
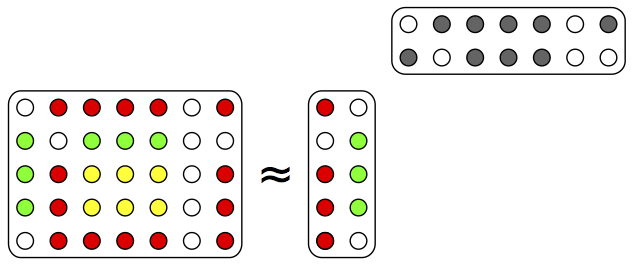
Data is often available in matrix form, in which columns are samples, and processing of such data often entails finding an approximate factorisation of the matrix in two factors. The first factor yields recurring patterns characteristic of the data. The second factor describes in which proportions each data sample is made of these patterns. Latent factor estimation (LFE) is the problem of finding such a factorisation, usually under given constraints. LFE appears under other domain-specific names such as dictionary learning, low-rank approximation, factor analysis or latent semantic analysis. It is used for tasks such as dimensionality reduction, unmixing, soft clustering, coding or matrix completion in very diverse fields.

In this project, we propose to explore three new paradigms that push the frontiers of traditional LFE. The first objective is to break beyond the ubiquitous Gaussian assumption, a practical choice that too rarely complies with the nature and geometry of the data. Estimation in non-Gaussian models is more difficult, but recent work in audio and text processing has shown that it pays off in practice. Second, in traditional settings the data matrix is often a collection of features computed from raw data. These features are computed with generic off-the-shelf transforms that loosely preprocess the data, setting a limit to performance. We propose to explore a new paradigm in which an optimal low-rank inducing transform is learnt together with the factors in a single step. Thirdly, we propose to reconsider the dominant deterministic approach to LFE and explore a novel statistical estimation paradigm, based on the marginal likelihood, with enhanced capabilities. The new methodology is applied to real-world problems in audio signal processing (speech enhancement, music remastering), remote sensing (Earth observation, cosmic object discovery) and data mining (multimodal information retrieval, user recommendation).

Latent factor estimation (LFE)

General principle of LFE

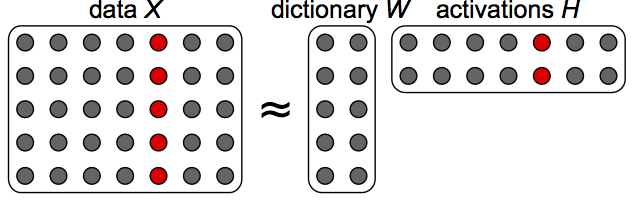
LFE for dimensionality reduction (e.g., coding, low-dimensional embedding)

LFE for matrix completion (e.g., collaborative filtering, inpainting)

LFE for unmixing (e.g., source separation, latent topic discovery)

Images copyright: C. Févotte

Examples of data & applications considered in the project

Spectral analysis

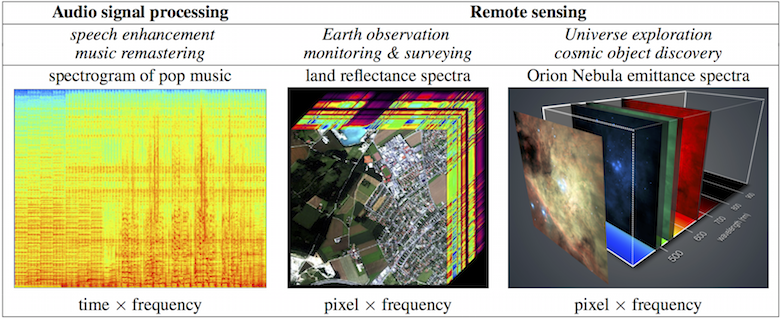Image credits: NASA/Aviris instrument (center) & ESO/Muse instrument (right). Music data excerpt: God Only Knows by the Beach Boys.

Data mining

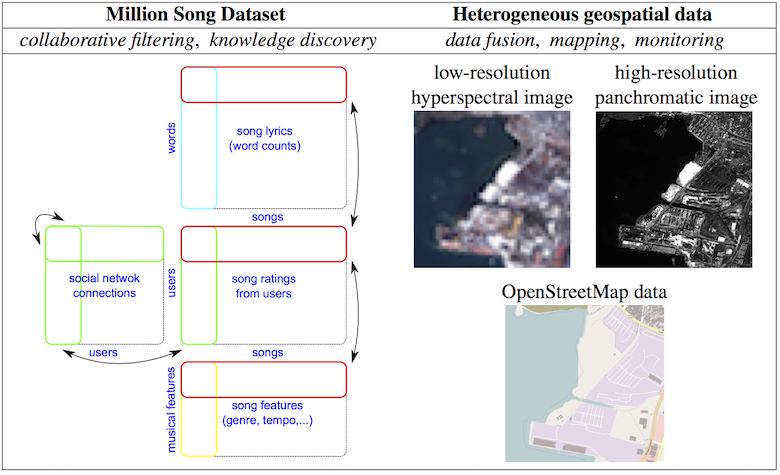
Images credit: DigitalGlobe